今回は、平面図形が苦手な子が、好きになって楽しく解けてしかも無理なく正解できる学習法を説明したいと思います。
ステップ1 フリーハンドできれいに図をかけるようになろう!
今まで見てきて、フリーハンドで図形をきれいにかけるのに図形問題が苦手な子はほとんどいないと言っても過言ではないです。
そして、フリーハンドで図形がきれいにかけるようになると図形に対する苦手意識が減って得意になる傾向も見られます。
というわけで、まずは美しく図をかけるようになることが大切なのです。
図形の周囲を円が移動するタイプ
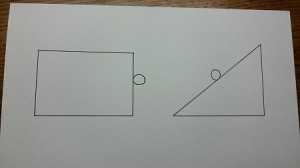
こんな問題がちょうど日能研のステージⅣの31回にあると思います(超具体的)。
(1)円の中心が動いた距離を求め、さらに(2)円が動いた面積を出す問題です。
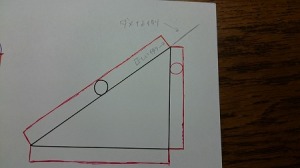
右の図なら、答えの図はこのようになるはずです。
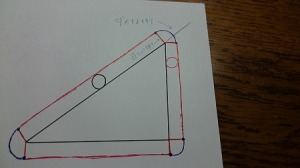
長方形の周辺を回る場合のかきかた
では、まずは長方形からかいていきましょう。
ここで、苦手な子や下手な子は、いきなり円の中心が動いた軌跡を直接書き込んでしまいます。
そして四隅がきれいにかけません。
ですから、少々セコいですが、まずは四隅を無視して、四辺の部分だけ、円の通った面積を図にかきます。
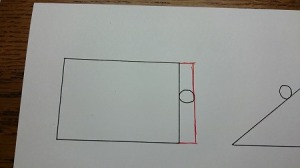
ポイントは、まず長方形の辺を伸ばします。
円の幅くらいまで伸ばします。
それを両端やってから最後につなぎます。
これを四辺すべて行います。
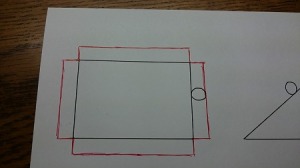
すると上の図のようになると思います。
そうしたら、辺の端同士をつないで扇形の弧をかきたします。
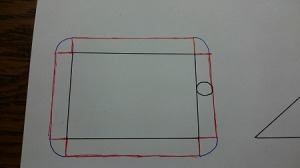
少々わかりにくいですが、赤が辺から長方形をつくったところ、青が最後にかきたした扇形の弧の部分です。
円の通った跡の面積は、長方形4つ+扇形4つという式になります。
素直にまじめにかくより、こちらのほうが簡単ですよね。
三角形の周辺を回る場合のかきかた
三角形の場合は長方形より難しいので、気をつけるところがあります。
ですから、手順をもうすこし丁寧にみていきましょう。
手順1:辺の両端を円の幅に伸ばす
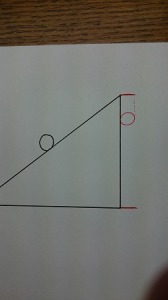
赤く書いた円が接している辺の上下を、円の幅に伸ばしています。
手順2:円と接するように両端をつないで長方形をつくる
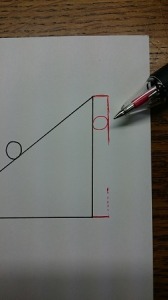
上下の伸ばした部分をつなぎます。このとき、円と接するようにしてください。
これで長方形の完成です。
手順3:次の両端は、先に作った長方形の辺と同じ分だけ伸ばす
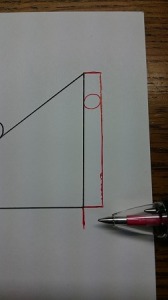
先につくった方をみながら、同じ長さになるように意識して辺をかきます。
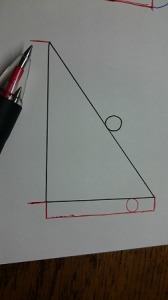
両端をかきました。
手順4:二つ目の長方形を完成させる
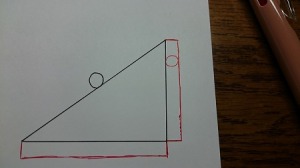
長方形がふたつ完成しました。
手順5:斜辺の両端の伸ばし方は要注意! ★円の幅と同じ幅を同じ方向に伸ばす!!
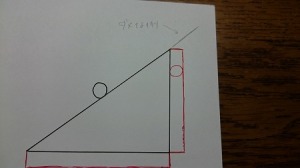
上はだめな例です。正確にいうと、これでも正しく書けば間違いではないのですが、これを使うと扇形を二つ作らないといけなくなります。ので、
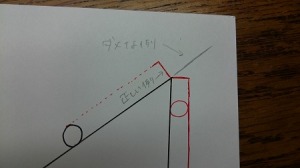
このように、基本にたちかえって、円の幅と同じ幅を同じ方向に伸ばすようにしましょう。
手順6:長方形を辺の数(今回は3つ)完成させる
さて、同様に長方形を作り、みっつの長方形が完成しました。
手順7:扇形をきれいにかくために点をつくる

長方形の端、扇形の弧のスタート地点になる部分にぐりぐりと点を書き入れます。これがあるとずいぶん違います。
手順8:扇形を完成させます。

かけました。同様に3箇所かいていきます。

完成しました。面積の式は、長方形3つ+扇形3つとなります。
図がきれいにかけない場合、なんどでもかかせます。定規は使ってはいけません。なぜならテスト本番、入試本番は定規使用不可だからです。
ステップ2 分配法則を利用しよう
先ほど、長方形の図の場合、長方形4つ+扇形4つと書きましたが…

円の半径を1cm、元の長方形の辺を6cmと8cmとしましょう。通った部分の面積を式にしていくと…
長方形部分は、6×2と8×2の2種類があることがわかります。
ですから、丁寧な式にすると、(6×2)×2+(8×2)×2です。
扇形は、90度ですから、(2×2×3.14×1/4)×4ですね。
つまり、この面積は、6×2×2+8×2×2+2×2×3.14×4×1/4という一本の式で表せます。
扇形の部分は先に4×1/4を相殺して消してよいです。すると、A+B+Cの形のどこにも2×2があることがわかります。
(6+8+3.14)×2×2=(14+3.14)×4=17.14×4 となって、めんどくさい計算は1回ですみます。
理論上は分配法則のほうがはやいですが、実際この問題の場合は、2×2×3.14が簡単です。
それなりのレベルにあれば、4×3.14=12.56を暗記していることが多いので、普通に前から計算したほうがはやいとおもいます。
その場合、(6+8)×2×2+12.56になり、14×4+12.56で答えが出ることになります。
ステップ3 扇形を合体すると円何個分かを理解しよう
よく、「これは円1個になるから~」と何の根拠もなくいう子がいます。
これは例題レベルならいいですが、もう少し難しくなると、なんでも1個分だと思ったり2個分だと目算したりして解けなくなります。
もうすこしちゃんと理由を見ていきましょう。

さて、突然ですが、三角形の内角の和はいくつでしょう。180度ですね。
では四角形は?360度ですね。
五角形は?540度ですね。
180ずつ増えます。
では、外角の和はどうでしょうか?…どんな図形でも180度ですね。
今回の場合は、外角を使ってもいいですが、せっかく長方形をかいているので、もっと素直にいきましょう。

まず、上の三角形を30・60・90の三角形だとします。左下が30度、右上が60度です。
360度から、三角形の中の角度と両脇の長方形の隅(90度)を引くと扇形の角度になるので、360-90×2-30=150、360-90×2-60=120、最後に右下は当然90ですが、これも、360-90×2-90=90となります。
よって、三つの扇形を足すと360度になり、円1個分と一緒になります。
さいごに
図形問題は、まずその図形をかくところからはじめましょう。
上手にかくためには、定規はいりません。ちょっとした工夫で、同じ長さのところは同じ長さに、同じ角度のところは同じ角度にみえるようにこころがければ上手にかけるようになります。
図形が苦手なみなさん、カリテがんばってくださいね。
*関連記事*








